Unit 11 homework 5 surface area of prisms and cylinders – In the realm of geometry, unit 11 homework 5 delves into the intriguing world of surface area, where prisms and cylinders take center stage. This exploration unveils the fundamental concepts and practical applications of surface area, inviting learners to engage with these captivating shapes.
From understanding the concept of surface area for prisms to deriving the formula for calculating the surface area of a cylinder, this homework assignment provides a comprehensive understanding of these geometric entities. Moreover, it delves into the practical applications of surface area, showcasing its significance in fields such as architecture, engineering, and packaging.
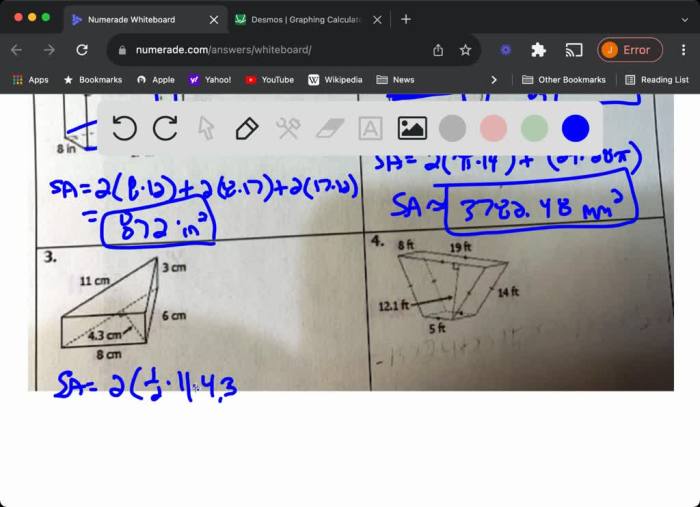
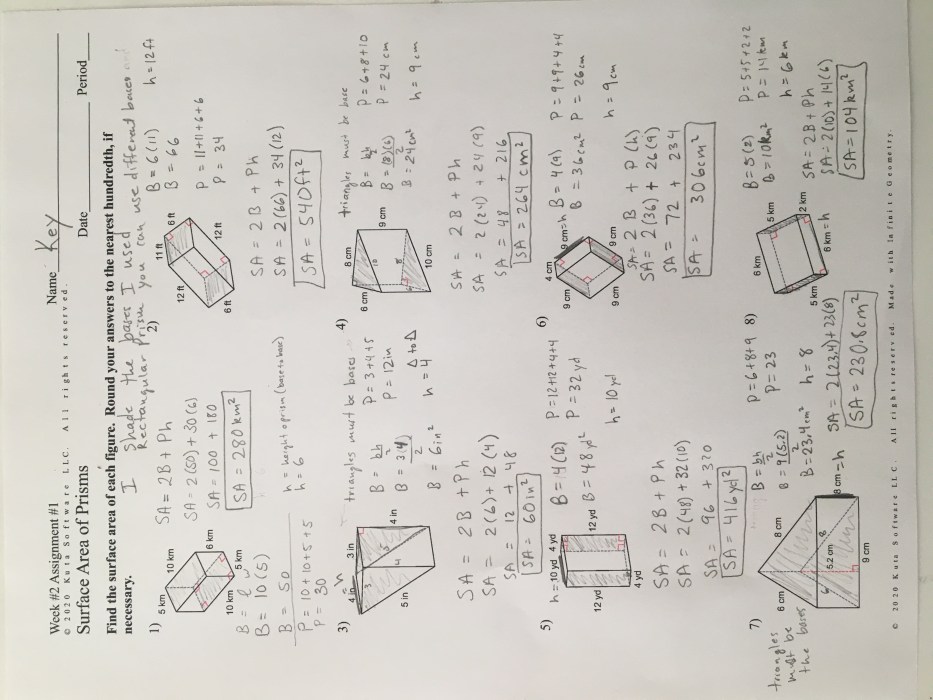
Surface Area of Prisms

The surface area of a prism is the sum of the areas of all its faces. For a rectangular prism, the surface area is given by the formula: 2(lw + lh + wh), where l is the length, w is the width, and h is the height.
For a triangular prism, the surface area is given by the formula: 2(1/2 bh + lw + lh), where b is the base length, h is the height, l is the length, and w is the width.
The following table summarizes the formulas for surface area of prisms:
| Prism Type | Formula |
|---|---|
| Rectangular Prism | 2(lw + lh + wh) |
| Triangular Prism | 2(1/2 bh + lw + lh) |
Surface Area of Cylinders
The surface area of a cylinder is the sum of the areas of its two circular bases and its lateral surface. The lateral surface area is the area of the curved surface of the cylinder.
The surface area of a cylinder is given by the formula: 2πrh + 2πr², where r is the radius of the base and h is the height.
The following diagram illustrates the formula for the surface area of a cylinder:
[Diagram of a cylinder with labeled radius and height]
Applications of Surface Area
- Architecture: Surface area is used to calculate the amount of paint or other materials needed to cover a building.
- Engineering: Surface area is used to calculate the heat transfer rate of a heat exchanger.
- Packaging: Surface area is used to determine the amount of material needed to package a product.
Comparing Surface Areas
The surface areas of different prisms and cylinders can be compared by using the formulas for surface area.
Factors that affect the surface area of these shapes include the length, width, height, and radius.
The following table compares the surface areas of different shapes with varying dimensions:
| Shape | Dimensions | Surface Area |
|---|---|---|
| Rectangular Prism | l = 5 cm, w = 3 cm, h = 2 cm | 52 cm² |
| Triangular Prism | b = 4 cm, h = 3 cm, l = 5 cm, w = 2 cm | 46 cm² |
| Cylinder | r = 2 cm, h = 5 cm | 62.83 cm² |
Problem-Solving with Surface Area
Word problems involving the surface area of prisms and cylinders can be solved by using the formulas for surface area.
Here is a step-by-step solution to a sample problem:
A rectangular prism has a length of 5 cm, a width of 3 cm, and a height of 2 cm. What is the surface area of the prism?
Step 1: Identify the formula for the surface area of a rectangular prism: 2(lw + lh + wh)
Step 2: Substitute the given values into the formula: 2(5 cm x 3 cm + 5 cm x 2 cm + 3 cm x 2 cm)
Step 3: Calculate the surface area: 2(15 cm² + 10 cm² + 6 cm²) = 52 cm²
Therefore, the surface area of the prism is 52 cm².
Here are some practice problems for students to solve:
- Find the surface area of a triangular prism with a base length of 4 cm, a height of 3 cm, a length of 5 cm, and a width of 2 cm.
- Find the surface area of a cylinder with a radius of 2 cm and a height of 5 cm.
Question & Answer Hub: Unit 11 Homework 5 Surface Area Of Prisms And Cylinders
What is the formula for calculating the surface area of a rectangular prism?
2(lw + lh + hw)
How is the surface area of a cylinder different from that of a prism?
A cylinder has a curved surface in addition to the two circular bases, while a prism has only flat surfaces.
What are some real-world applications of surface area?
Calculating the surface area of buildings for painting or insulation, designing packaging for products, and determining the surface area of materials used in engineering.